The Class 8 is an important year in a student’s life and Maths is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 8 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete NCERT Class 8 Maths Book syllabus.
(i) Quadrilateral ABCD AB = 4.5 cm
BC = 5.5 cm
CD = 4 cm AD = 6 cm AC = 7 cm
Solution:
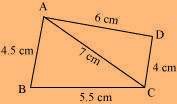The rough sketch of the quadrilateral ABCD can be drawn as follows.
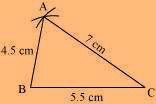
(1) ∆ABC can be constructed by using the given measurements as follows.
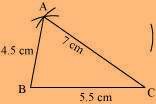
(2) Vertex D is 6 cm away from vertex A. Therefore, while taking A as the centre, draw an arc of radius 6 cm.
(3) Taking C as the centre, draw an arc of radius 4 cm, cutting the previous arc at point D. Joint D to A and C.
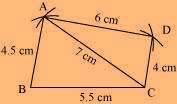
ABCD is the required quadrilateral.
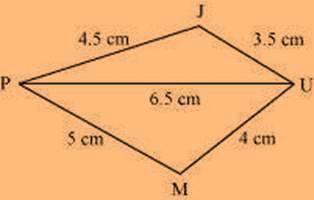
UM = 4 cm MP = 5 cm PJ = 4.5 cm PU = 6.5 cm
Solution:
The rough sketch of the quadrilateral JUMP can be drawn as follows.
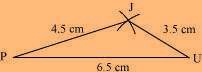
(1) ∆ JUP can be constructed by using the given measurements as follows.
(2) Vertex M is 5 cm away from vertex P and 4 cm away from vertex U. Taking P and U as centres, draw arcs of radii 5 cm and 4 cm, respectively. Let the point of intersection be M.
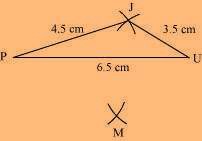
(3) Join M to P and U.
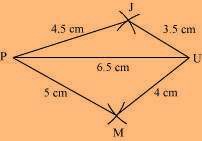
JUMP is the required quadrilateral.
(iii) Parallelogram MORE
OR = 6 cm
Solution:
RE = 4.5 cm
EO = 7.5
We know that opposite sides of a parallelogram are equal in length, and also, these are parallel to each other.
i.e., ME = OR, MO = ER
The rough sketch of the parallelogram MORE can be drawn as follows.
(1) ∆ EOR can be constructed by using the given measurements as follows.
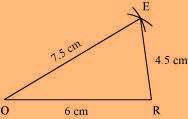
(2) Vertex M is 4.5 cm away from vertex O and 6 cm away from vertex E. Therefore, while taking O and E as centres, draw arcs of 4.5 cm radius and 6 cm radius, respectively. These will intersect each other at point M.
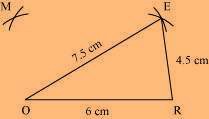
(3) Join M to O and E.
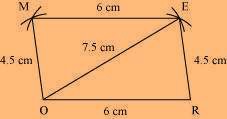
MORE is the required parallelogram.
(iv) Rhombus BEST
BE = 4.5 cm
ET = 6 cm
Solution:
We know that all sides of a rhombus are of the same measure. Hence, BE = ES = ST = TB
The rough sketch of the rhombus BEST can be drawn as follows.
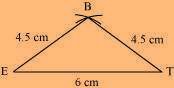(1) ∆ BET can be constructed by using the given measurements as follows.
(2) Vertex S is 4.5 cm away from vertex E and also from vertex T. Therefore, while taking E and T as centres, draw arcs of 4.5 cm radius, which will intersect each other at point S.
(3) Join S to E and T.
NCERT Solution For Class 8 Maths Chapter 4 Image
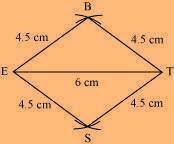
BEST is the required rhombus.
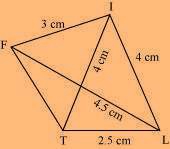
(i) Quadrilateral LIFT LI = 4 cm
IF = 3 cm TL = 2.5 cm LF = 4.5 cm
IT = 4 cm
Solution:
A rough sketch of the quadrilateral LIFT can be drawn as follows.
(1) ∆ ITL can be constructed by using the given measurements as follows.
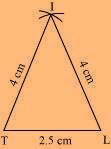
(2) Vertex F is 4.5 cm away from vertex L and 3 cm away from vertex I. ∴ while taking L and I as centres, draw arcs of 4.5 cm radius and 3 cm radius, respectively, which will intersect each other at point F.
(3) Join F to T and F to I.
LIFT is the required quadrilateral.
GL = 6 cm GD = 6 cm LD = 5 cm OD = 10 cm
Solution:
The rough sketch of the quadrilateral GOLD can be drawn as follows.
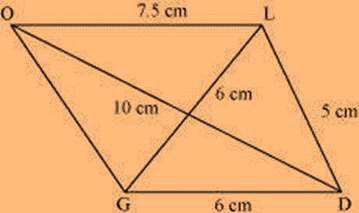
(1) ∆ GDL can be constructed by using the given measurements as follows.
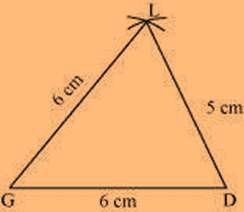
(2) Vertex O is 10 cm away from vertex D and 7.5 cm away from vertex L. Therefore, while taking D and L as centres, draw arcs of 10 cm radius and 7.5 cm radius, respectively. These will intersect each other at point O.
(3) Join O to G and L.
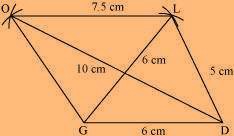
GOLD is the required quadrilateral.
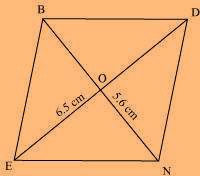
(iii) Rhombus BEND
BN = 5.6 cm
DE = 6.5 cm
Solution:
We know that the diagonals of a rhombus always bisect each other at 90º.
Let us assume that these are intersecting each other at point O in this rhombus. Hence, EO = OD = 3.25 cm
The rough sketch of the rhombus BEND can be drawn as follows.
(1) Draw a line segment BN of 5.6 cm, and also draw its perpendicular bisector. Let it intersect the line segment BN at point O.
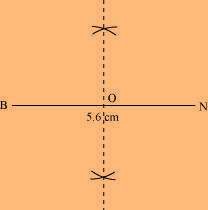
(2) Taking O as the centre, draw arcs of 3.25 cm radius to intersect the perpendicular bisector at points D and E.
(3) Join points D and E to points B and N.
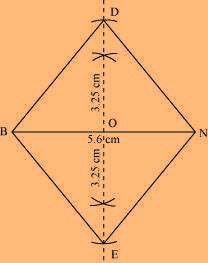
BEND is the required quadrilateral.
(i) Quadrilateral MORE MO = 6 cm
OR = 4.5 cm
∠M = 60°
∠O = 105°
∠R = 105°
Solution:
Rough Figure:
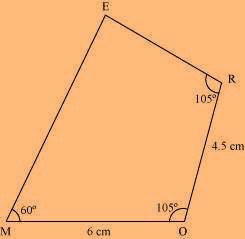
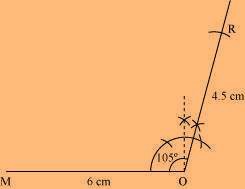(1) Draw a line segment MO of 6 cm and an angle of 105º at point O. As vertex R is 4.5 cm away from the vertex O, cut a line segment OR of 4.5 cm from this ray.
(2) Again, draw an angle of 105º at point R.
(3) Draw an angle of 60º at point M. Let this ray meet the previously drawn ray from R at point E.
MORE is the required quadrilateral.
LA = 6.5 cm
∠P = 90°
∠A = 110°
∠N = 85°
Solution:
The sum of the angles of a quadrilateral is 360°. In quadrilateral PLAN,
∠P + ∠L + ∠A + ∠N = 360° 90° + ∠L + 110° + 85° = 360°
285° + ∠L = 360°
∠L = 360° − 285° = 75°
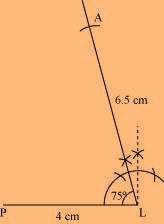
Rough Figure:
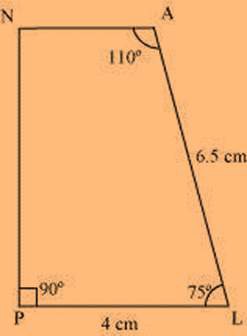
(1) Draw a line segment PL of 4 cm and draw an angle of 75º at point L. As vertex A is 6.5 cm away from vertex L, cut a line segment LA of 6.5 cm from this ray.
(2) Again, draw an angle of 110º at point A.
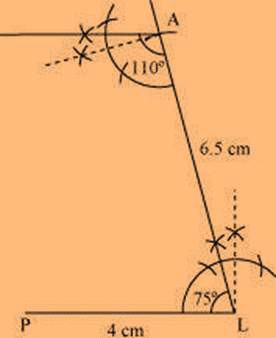
(3) Draw an angle of 90º at point P. This ray will meet the previously drawn ray from A at point N.
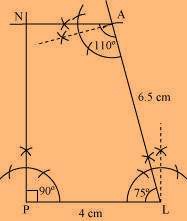
PLAN is the required quadrilateral.
EA = 6 cm
∠R = 85°
Solution:
Rough Figure:
(1) Draw a line segment HE of 5 cm and an angle of 85º at point E. As vertex A is 6 cm away from vertex E, cut a line segment EA of 6 cm from this ray.
(2) Vertex R is 6 cm and 5 cm away from vertex H and A, respectively. By taking radii as 6 cm and 5 cm, draw arcs from points H and A, respectively. These will intersect each other at point R.
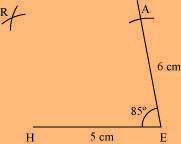
(3) Join R to H and A.
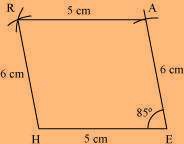
HEAR is the required quadrilateral.
OK = 7 cm KA = 5 cm
Solution:
Rough Figure:
(1) Draw a line segment OK of 7 cm and an angle of 90º at point K. As vertex A is 5 cm away from vertex K, cut a line segment KA of 5 cm from this ray.
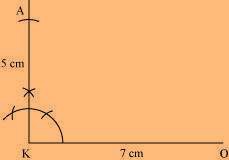
(2) Vertex Y is 5 cm and 7 cm away from vertex O and A, respectively. By taking
radii as 5 cm and 7 cm, draw arcs from points O and A, respectively. These will intersect each other at point Y.
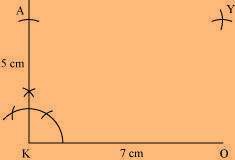
(3) Join Y to A and O.
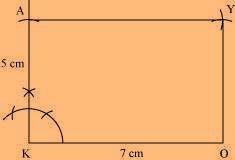
OKAY is the required quadrilateral.
(i) Quadrilateral DEAR DE = 4 cm
EA = 5 cm AR
= 4.5 cm
∠E = 60°
∠A = 90°
Solution:
Rough Figure:
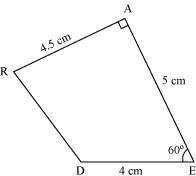
(1) Draw a line segment DE of 4 cm and an angle of 60º at point E. As vertex A is 5 cm away from vertex E, cut a line segment EA of 5 cm from this ray.
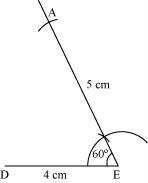
(2) Again, draw an angle of 90º at point A. As vertex R is 4.5 cm away from vertex A, cut a line segment RA of 4.5 cm from this ray.
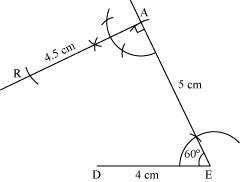
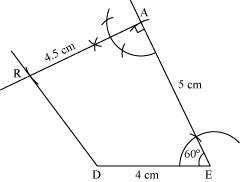(3) Join D to R.
DEAR is the required quadrilateral.
RU = 3 cm UE = 4 cm
∠R = 75°
∠U = 120°
Solution:
Rough Figure:
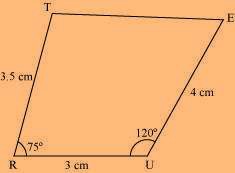
(1) Draw a line segment RU of 3 cm and an angle of 120º at point U. As vertex E is 4 cm away from vertex U, cut a line segment UE of 4 cm from this ray.
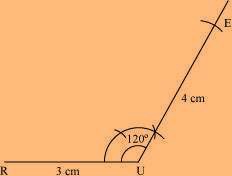
(2) Next, draw an angle of 75º at point R. As vertex T is 3.5 cm away from vertex R, cut a line segment RT of 3.5 cm from this ray.
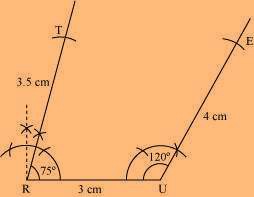
(3) Join T to E.
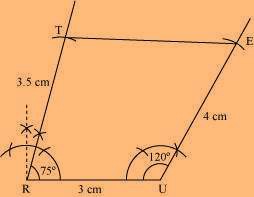
TRUE is the required quadrilateral.
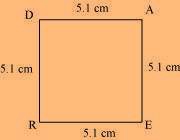
1. The square READ with RE = 5.1 cm
Solution:
All the sides of a square are of the same measure, and also, all the interior angles of a square are 90º measure. Therefore, the given square READ can be drawn as follows.
Rough Figure:
(1) Draw a line segment RE of 5.1 cm and an angle of 90º at points R and E.
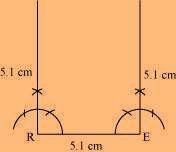
(2) As vertex A and D are 5.1 cm away from vertex E and R, respectively, cut line segments EA and RD, each of 5.1 cm from these rays.
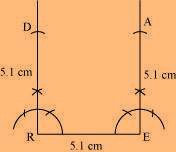
(3) Join D to A.
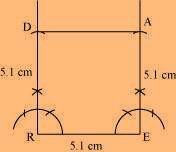
READ is the required square.
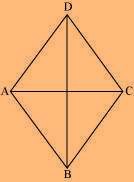Rough Figure:
(1) Draw a line segment AC of 5.2 cm and draw its perpendicular bisector. Let it intersect the line segment AC at point O.
(2) Draw arcs of 6.4/2 = 3.2 on both sides of this perpendicular bisector. Let the arcs intersect the perpendicular bisector at points B and D.
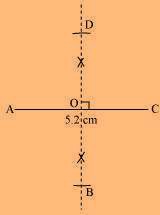
(3) Join points B and D with points A and C.
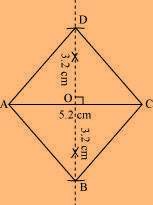
ABCD is the required rhombus.
Rough figure:
(1) Draw a line segment AB of 5 cm and an angle of 90º at points A and B.
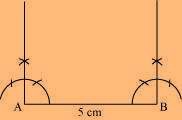
(2) As vertex C and D are 4 cm away from vertex B and A, respectively, cut line segments AD and BC, each of 4 cm, from these rays.
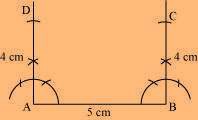
(3) Join D to C.
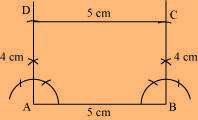
ABCD is the required rectangle.
4. A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm. Solution:
Opposite sides of a parallelogram are equal and parallel to each other. The given parallelogram OKAY can be drawn as follows.
Rough Figure:
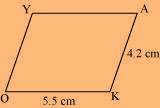
(1) Draw a line segment OK of 5.5 cm and a ray at point K at a convenient angle.
(2) Draw a ray at point O parallel to the ray at K. As the vertices A and Y are 4.2 cm away from the vertices K and O, respectively, cut line segments KA and OY, each of 4.2 cm, from these rays.
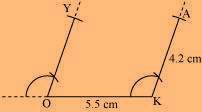
(3) Join Y to A.
OKAY is the required rectangle.
Learning the chapter Practical Geometry enables the students to: